迭代
— 焉知非鱼Iterations
迭代 #
迭代算法出现在数据分析的许多领域,如机器学习或图形分析。为了实现大数据的承诺,从数据中提取有意义的信息,此类算法至关重要。随着人们对在非常大的数据集上运行这类算法的兴趣越来越大,就需要以大规模并行的方式执行迭代。
Flink 程序通过定义一个步骤函数并将其嵌入到一个特殊的迭代运算符中来实现迭代算法。这个运算符有两个变体。Iterate 和 Delta Iterate。这两个运算符都是在当前的迭代状态上反复调用步骤函数,直到达到某个终止条件。
在这里,我们提供了这两个操作符变体的背景,并概述了它们的用法。编程指南解释了如何在 Scala 和 Java 中实现这些操作符。我们还通过 Flink 的图处理 API Gelly 支持以顶点为中心的迭代和集和应用迭代。
下表提供了这两种运算符的概述:
| Iterate | Delta Iterate | |
|---|---|---|
| Iteration 输入 | Partial Solution | Workset and Solution Set |
| Step 函数 | Arbitrary Data Flows | Arbitrary Data Flows |
| State Update | Next partial solution | Next workset,Changes to solution set |
| Iteration Result | Last partial solution | Solution set state after last iteration |
| Termination | Maximum number of iterations (default),Custom aggregator convergence | Maximum number of iterations or empty workset (default),Custom aggregator convergence |
Iterate Operator #
迭代运算符涵盖了简单的迭代形式:在每一次迭代中,step 函数都会消耗整个输入(上一次迭代的结果,或初始数据集),并计算出下一个版本的部分解(如 map, reduce, join 等)。
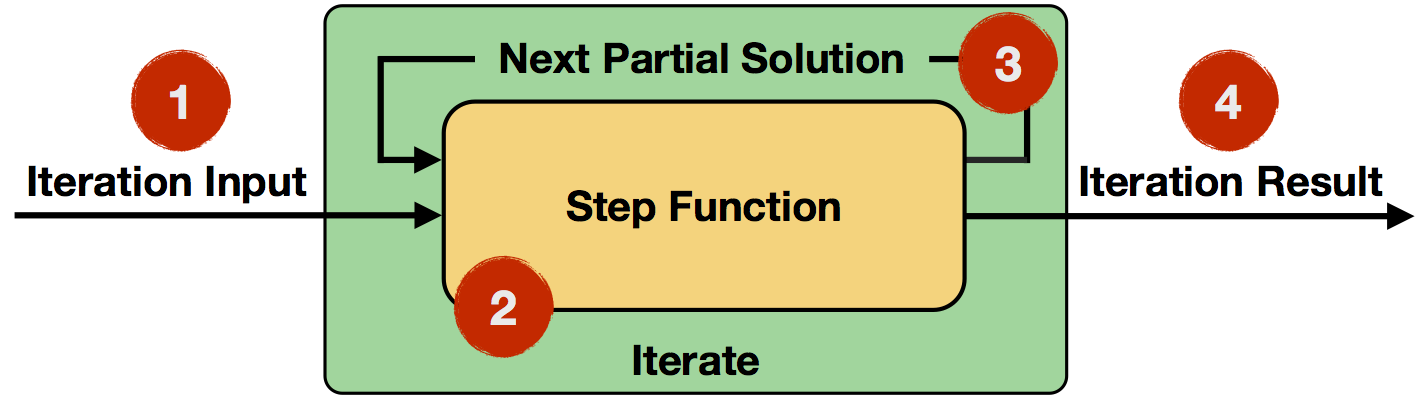
- 迭代输入。第一次迭代的初始输入,来自数据源或之前的运算符。
- step 函数。步骤函数将在每次迭代中执行。它是一个任意的数据流,由 map、reduce、join 等运算符组成,取决于你手头的具体任务。
- 下一个部分解决方案。在每次迭代中,步骤函数的输出将被反馈到下一次迭代中。
- 迭代结果。上一次迭代的输出会被写入数据接收器,或者作为后续运算符的输入。
有多个选项可以指定迭代的终止条件。
- 最大迭代次数。没有任何进一步的条件,迭代将被执行这么多次。
- 自定义聚合器收敛。迭代允许指定自定义聚合器和收敛标准,比如对发出的记录数量进行加总(聚合器),如果这个数字为零就终止(收敛标准)。
你也可以用伪代码来思考迭代操作符。
IterationState state = getInitialState();
while (!terminationCriterion()) {
state = step(state);
}
setFinalState(state);
详情和代码示例请参见编程指南。
例子: 数字递增 #
在下面的例子中,我们对一组数字进行迭代递增。
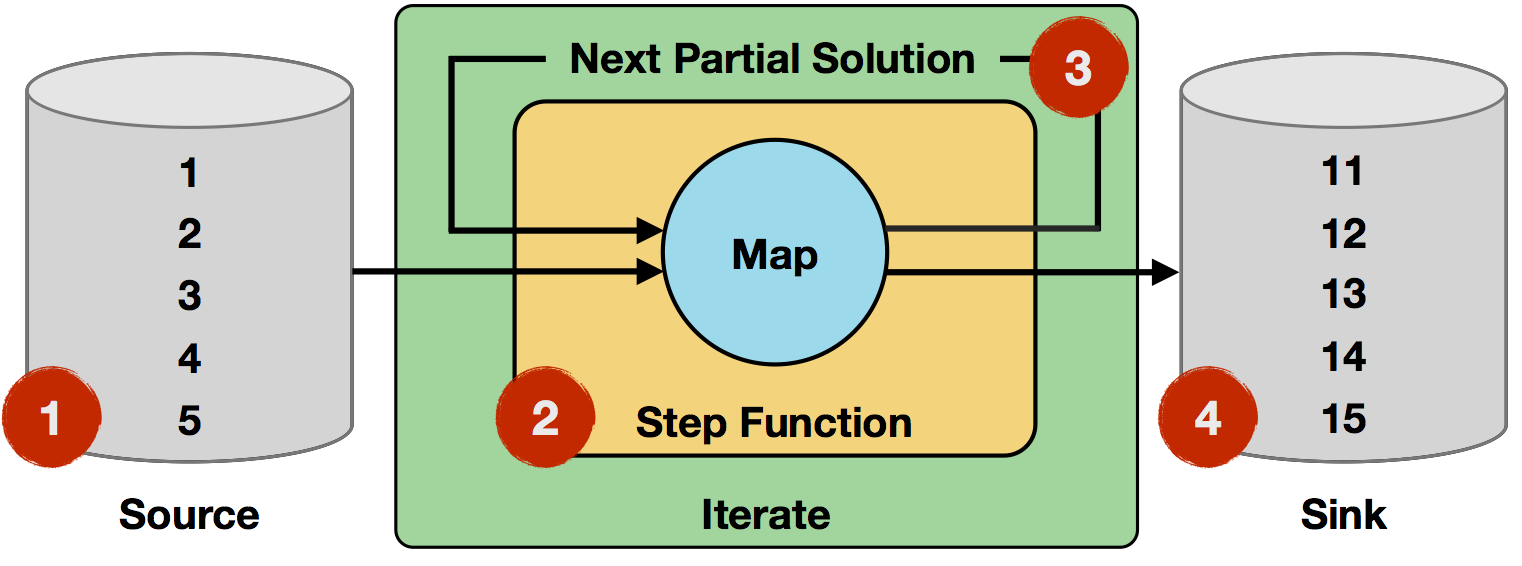
- 迭代输入。初始输入是从数据源读取的,由5个单字段记录组成(整数1至5)。
- step 函数。步进函数是一个单一的 map 运算符,它将整数字段从i递增到i+1。它将被应用于输入的每一条记录。
- 下一个部分解。step 函数的输出将是 map 运算符的输出,也就是整数递增的记录。
- 迭代结果。经过十次迭代,初始数字将被递增十倍,结果是整数11到15。
// 1st 2nd 10th
map(1) -> 2 map(2) -> 3 ... map(10) -> 11
map(2) -> 3 map(3) -> 4 ... map(11) -> 12
map(3) -> 4 map(4) -> 5 ... map(12) -> 13
map(4) -> 5 map(5) -> 6 ... map(13) -> 14
map(5) -> 6 map(6) -> 7 ... map(14) -> 15
请注意,1、2和4可以是任意的数据流。
增量迭代运算符 #
delta 迭代算子涵盖了增量迭代的情况。增量迭代有选择地修改其解的元素,并对解进行演化,而不是完全重新计算。
在适用的情况下,这将导致更高效的算法,因为在每次迭代中,并不是解集中的每个元素都会改变。这样就可以把注意力集中在解的热点部分,而对冷点部分不加处理。通常情况下,大部分解的冷却速度比较快,后面的迭代只对一小部分数据进行操作。
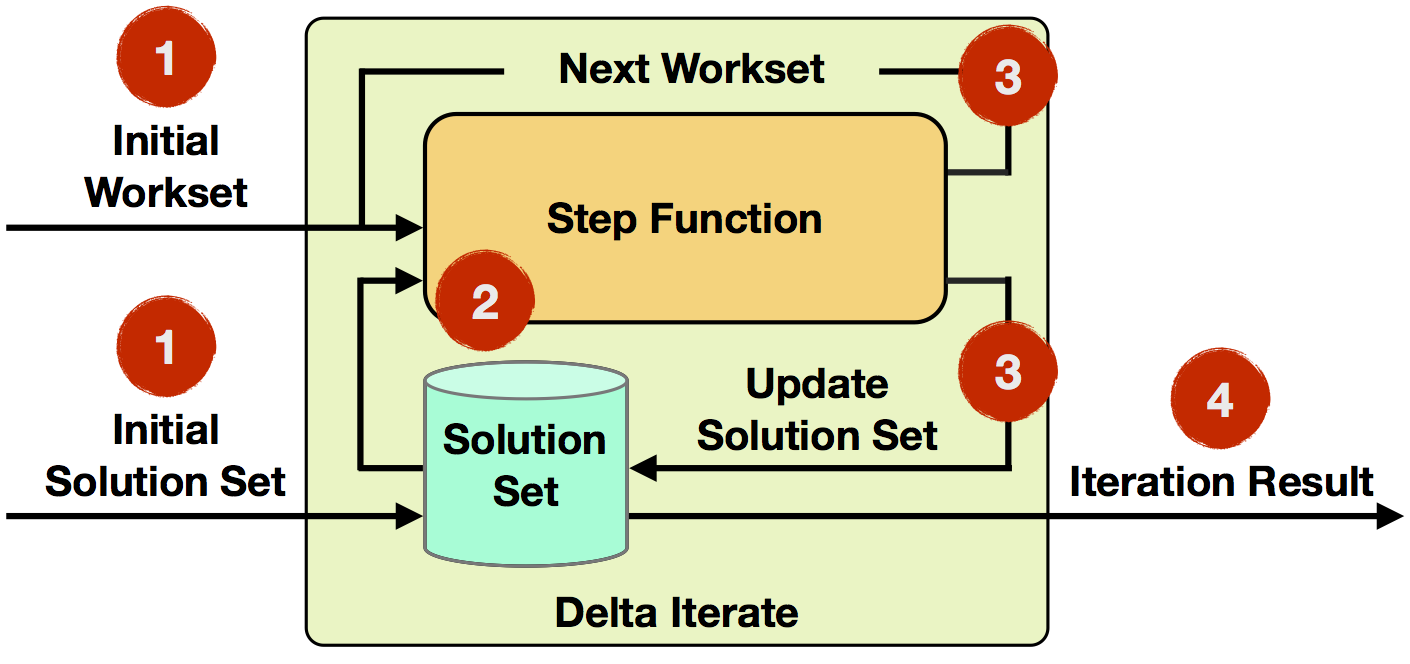
- 迭代输入。从数据源或以前的运算符中读取初始工作集和解决方案集,作为第一次迭代的输入。
- step 函数。在每次迭代中,步骤函数将被执行。它是一个任意的数据流,由 map、reduce、join 等运算符组成,取决于你手头的具体任务。
- 下一个工作集/更新解决方案集。下一个工作集驱动迭代计算,并将反馈到下一个迭代中。此外,解决方案集将被更新并隐式转发(它不需要被重建)。这两个数据集都可以通过步长函数的不同运算符进行更新。
- 迭代结果。最后一次迭代后,解集被写入数据接收器,或作为下面运算符的输入。
delta 迭代的默认终止条件由空工作集收敛准则和最大迭代次数指定。当产生的下一个工作集为空或达到最大迭代次数时,迭代将终止。也可以指定一个自定义的聚合器和收敛准则。
你也可以用伪代码来思考迭代操作符。
IterationState workset = getInitialState();
IterationState solution = getInitialSolution();
while (!terminationCriterion()) {
(delta, workset) = step(workset, solution);
solution.update(delta)
}
setFinalState(solution);
详情和代码示例请参见编程指南。
例子: 在图中传播最小值 #
在下面的例子中,每个顶点都有一个ID和一个着色。每个顶点将把它的顶点ID传播给邻近的顶点。目标是给子图中的每个顶点分配最小的ID。如果一个接收到的ID比当前的ID小,它就会改变成接收到ID的顶点的颜色。这在社区分析或连接组件计算中可以找到一个应用。
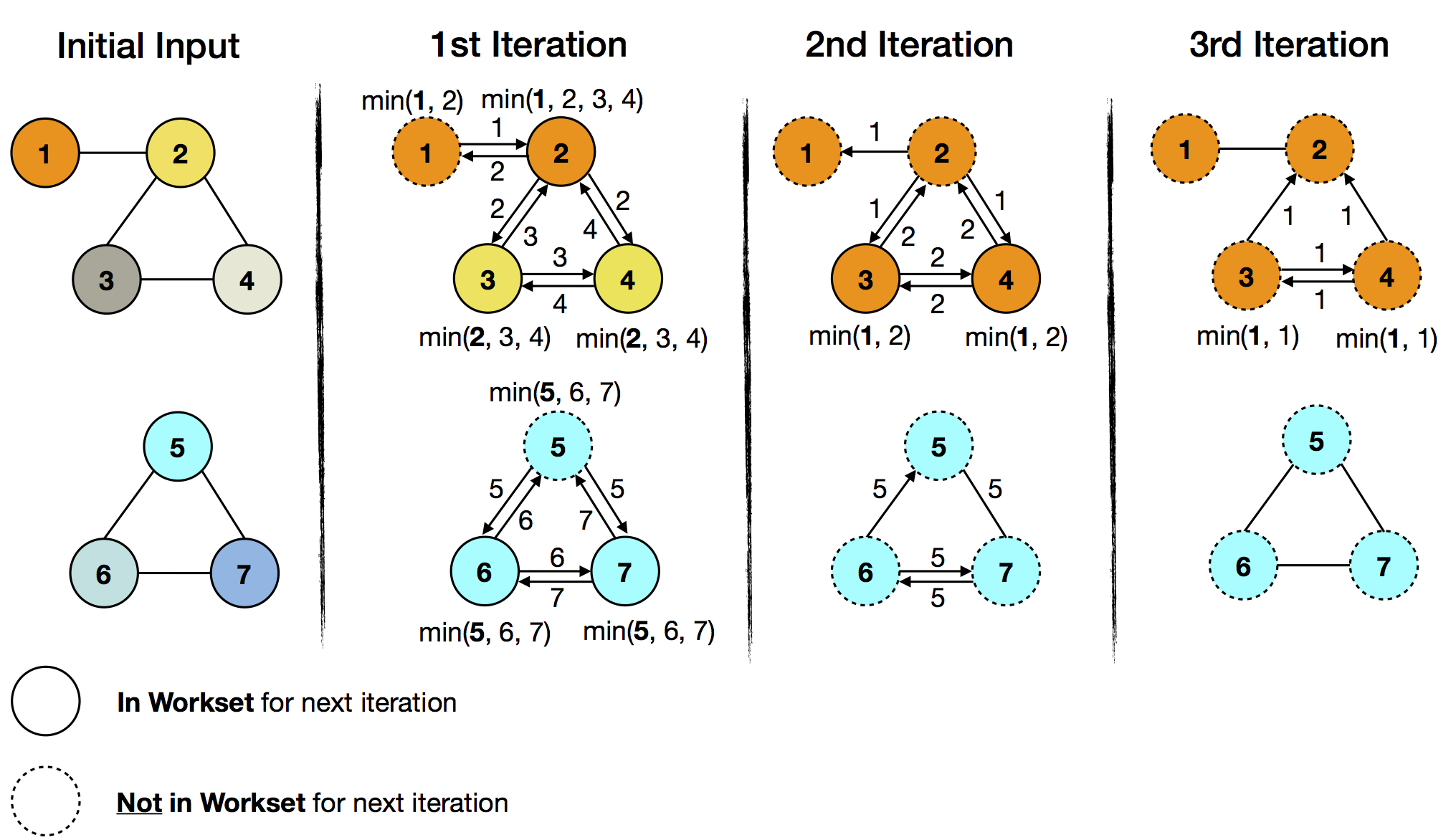
初始输入被设定为工作集和解决方案集。在上图中,颜色直观地显示了解决方案集的演变。随着每次迭代,最小ID的颜色在各自的子图中蔓延。同时,每一次迭代,工作量(交换和比较顶点ID)都在减少。这对应于工作集的大小递减,在三次迭代后,工作集从所有七个顶点变为零,此时迭代终止。重要的观察是,下半子图在上半子图之前收敛,而delta迭代能够用工作集抽象捕捉到这一点。
在上子图中,ID 1(橙色)是最小ID。在第一次迭代中,它将被传播到顶点2,随后它的颜色将变为橙色。顶点3和4将收到ID 2(黄色)作为它们当前的最小ID,并改变为黄色。因为顶点1的颜色在第一次迭代中没有改变,所以在下一个工作集中可以跳过它。
在下层子图中,ID 5(青色)是最小ID。下层子图的所有顶点都会在第一次迭代中收到它。同样,我们可以在下一个工作集中跳过没有变化的顶点(顶点5)。
在第2次迭代中,工作集大小已经从7个元素减少到5个元素(顶点2、3、4、6和7)。这些都是迭代的一部分,并进一步传播它们当前的最小ID。在这次迭代之后,下半部分子图已经收敛了(图的冷部分),因为它在工作集中没有元素,而上半部分则需要对剩下的两个工作集元素(顶点3和4)进行进一步的迭代(图的热部分)。
当第3次迭代后工作集为空时,迭代终止。
Superstep 同步 #
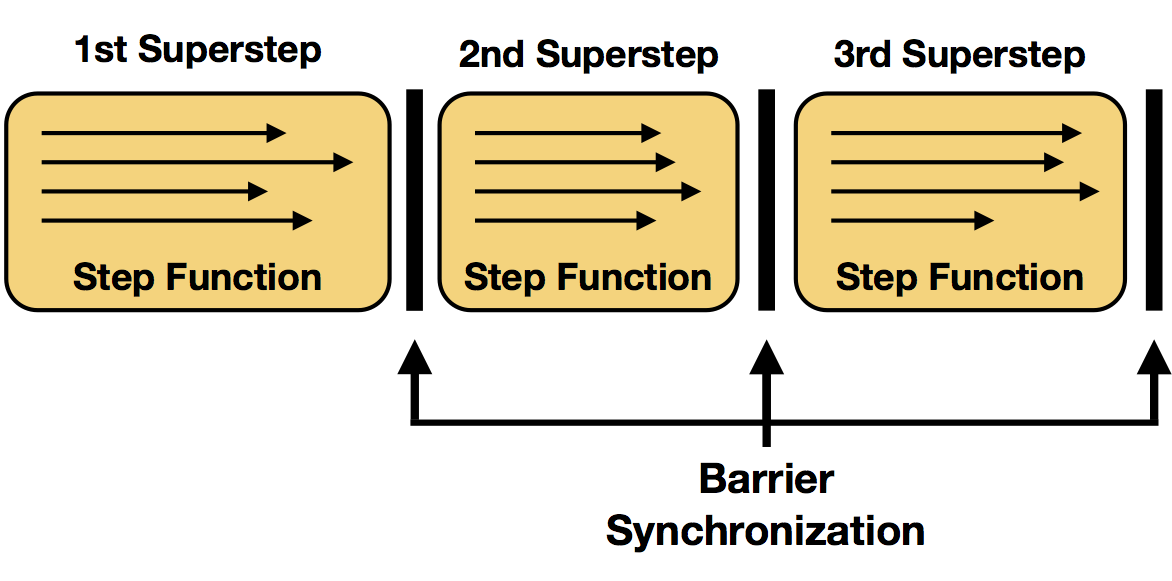
我们将迭代操作符的步骤函数的每次执行称为单次迭代。在并行设置中,步骤函数的多个实例在迭代状态的不同分区上并行评估。在许多设置中,在所有并行实例上对步骤函数的一次评估形成一个所谓的超级步骤,这也是同步的粒度。因此,一个迭代的所有并行任务都需要完成 superstep,才会初始化下一个 superstep。终止标准也将在 superstep 障碍处进行评估。
原文链接: https://ci.apache.org/projects/flink/flink-docs-release-1.11/dev/batch/iterations.html